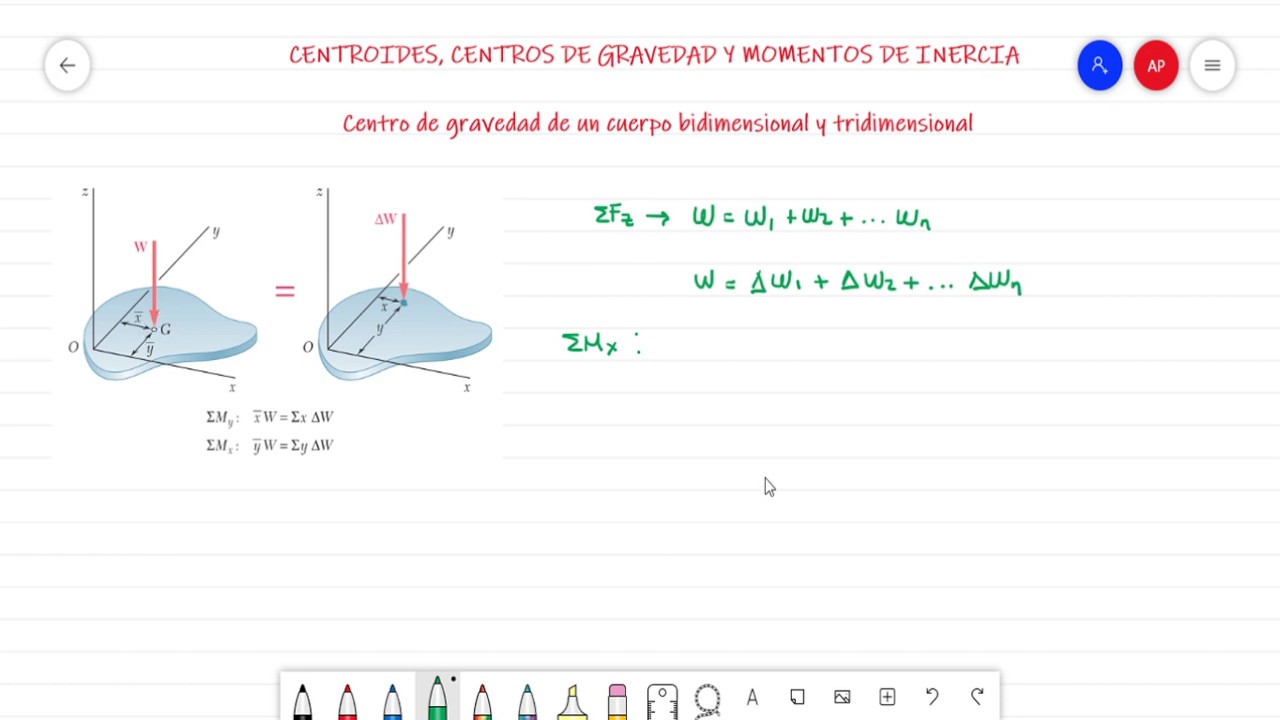
El centro de gravedad es un concepto fundamental en la física y la ingeniería que se refiere al punto en el que se puede considerar que está concentrada toda la masa de un objeto. En el caso de los cuerpos bidimensionales, como figuras geométricas, entender cómo calcular su centro de gravedad es esencial para diversas aplicaciones, desde el diseño arquitectónico hasta la mecánica. En este artículo, vamos a desglosar los pasos necesarios para calcular el centro de gravedad de un cuerpo bidimensional, así como los métodos más comunes y algunos ejemplos prácticos que te ayudarán a asimilar el concepto. Si alguna vez te has preguntado cómo determinar el equilibrio de un objeto plano o cómo afecta su forma a su estabilidad, este artículo es para ti.
¿Qué es el Centro de Gravedad?
El centro de gravedad de un cuerpo bidimensional se puede definir como el punto en el que se equilibran todas las fuerzas gravitacionales que actúan sobre él. En términos simples, es el «centro de masa» del objeto, aunque en el caso de cuerpos bidimensionales, este concepto se traduce en un punto en el plano donde la masa total puede ser considerada como concentrada. Este punto no solo es crucial en la física, sino que también tiene aplicaciones prácticas en ingeniería, diseño y arquitectura.
Importancia del Centro de Gravedad
Conocer el centro de gravedad de un cuerpo bidimensional es vital por varias razones:
- Estabilidad: Un objeto será más estable si su centro de gravedad se encuentra más bajo. Por ejemplo, un coche con un centro de gravedad bajo es menos propenso a volcarse.
- Equilibrio: Para que un objeto permanezca en equilibrio, su centro de gravedad debe estar alineado verticalmente sobre su base de soporte.
- Diseño y análisis: En la ingeniería y el diseño, entender cómo se distribuye la masa de un objeto puede influir en su rendimiento y funcionalidad.
Métodos para Calcular el Centro de Gravedad
Existen diferentes métodos para calcular el centro de gravedad de un cuerpo bidimensional, y la elección del método depende de la complejidad de la figura y de los datos disponibles. Aquí exploraremos dos de los métodos más comunes: el método de la suma de áreas y el método de la integración.
Método de la Suma de Áreas
Este método es especialmente útil para figuras simples y compuestas. La idea básica es dividir el cuerpo en formas más simples (como triángulos, rectángulos y círculos) y calcular el centro de gravedad de cada una de estas formas. Luego, se usa una fórmula para encontrar el centro de gravedad del cuerpo completo.
Los pasos son los siguientes:
- Dividir el cuerpo en formas geométricas simples.
- Calcular el área y el centro de gravedad de cada forma.
- Usar la fórmula para el centro de gravedad en coordenadas cartesianas:
- Xc = (Σ(Ai * xi)) / ΣAi
- Yc = (Σ(Ai * yi)) / ΣAi
Veamos un ejemplo práctico para ilustrar este método:
Supongamos que tenemos un cuerpo bidimensional que consiste en un rectángulo y un triángulo. Si el rectángulo tiene un área de 20 m² y su centro de gravedad está en (2, 3), y el triángulo tiene un área de 10 m² con su centro de gravedad en (5, 7), podemos calcular el centro de gravedad del cuerpo completo de la siguiente manera:
1. Calculamos las contribuciones de cada figura al centro de gravedad:
- Rectángulo: 20 m² * (2, 3) = (40, 60)
- Triángulo: 10 m² * (5, 7) = (50, 70)
2. Sumamos estas contribuciones:
- Σ(Ai * xi) = 40 + 50 = 90
- Σ(Ai * yi) = 60 + 70 = 130
3. Sumamos las áreas:
- ΣAi = 20 + 10 = 30
4. Finalmente, calculamos las coordenadas del centro de gravedad:
- Xc = 90 / 30 = 3
- Yc = 130 / 30 ≈ 4.33
Así, el centro de gravedad del cuerpo bidimensional está en aproximadamente (3, 4.33).
Método de Integración
Este método es más avanzado y se utiliza cuando el cuerpo tiene una forma irregular o cuando se necesita un cálculo más preciso. Consiste en integrar la función de densidad a lo largo de la figura. Este método se puede aplicar a cuerpos con densidad variable y permite obtener resultados más exactos.
Los pasos para aplicar el método de integración son los siguientes:
- Definir la función que describe la forma del cuerpo.
- Establecer los límites de integración.
- Calcular el centro de gravedad usando las integrales:
- Xc = (1/M) ∫ x * dA
- Yc = (1/M) ∫ y * dA
Para entender este método, consideremos un ejemplo simple donde tenemos una figura en forma de arco. La función que describe el arco puede ser compleja, pero con un software de cálculo, podemos integrar y obtener el centro de gravedad de la figura.
Ejemplos Prácticos de Cálculo del Centro de Gravedad
Calcular el centro de gravedad de diferentes figuras puede ser muy ilustrativo. Aquí veremos algunos ejemplos prácticos que te ayudarán a consolidar lo aprendido hasta ahora.
Ejemplo 1: Cálculo del Centro de Gravedad de un Triángulo
Consideremos un triángulo con vértices en (0, 0), (4, 0) y (2, 3). Para encontrar el centro de gravedad, seguimos estos pasos:
1. Calculamos el área del triángulo usando la fórmula:
Área = (base * altura) / 2 = (4 * 3) / 2 = 6 m².
2. Determinamos las coordenadas del centro de gravedad del triángulo, que se encuentran en el punto medio de cada lado:
- Xc = (x1 + x2 + x3) / 3 = (0 + 4 + 2) / 3 = 2.
- Yc = (y1 + y2 + y3) / 3 = (0 + 0 + 3) / 3 = 1.
Por lo tanto, el centro de gravedad del triángulo está en (2, 1).
Ejemplo 2: Cálculo del Centro de Gravedad de un Rectángulo
Imaginemos un rectángulo de 6 m de largo y 4 m de ancho. Sus vértices están en (0, 0), (6, 0), (6, 4) y (0, 4). El centro de gravedad se calcula fácilmente:
1. El área del rectángulo es:
Área = largo * ancho = 6 * 4 = 24 m².
2. Las coordenadas del centro de gravedad son simplemente el punto medio del rectángulo:
- Xc = largo / 2 = 6 / 2 = 3.
- Yc = ancho / 2 = 4 / 2 = 2.
Así que el centro de gravedad del rectángulo es (3, 2).
Factores que Afectan el Centro de Gravedad
El centro de gravedad de un cuerpo bidimensional no es una propiedad fija; puede variar en función de varios factores. Comprender estos factores es crucial para aplicaciones prácticas en la ingeniería y el diseño.
Forma del Objeto
La forma del objeto es uno de los principales factores que afecta el centro de gravedad. Por ejemplo, un objeto alargado como un palo tendrá un centro de gravedad diferente en comparación con un objeto compacto como una esfera. Esto se debe a que la distribución de masa es diferente en cada caso.
Distribución de Masa
La manera en que se distribuye la masa también influye en el centro de gravedad. Un objeto con una densidad uniforme tendrá un centro de gravedad diferente que uno con una densidad variable. Por ejemplo, si un lado de un triángulo es más pesado que el otro, su centro de gravedad se desplazará hacia el lado más pesado.
Posición y Orientación
La posición y la orientación del objeto también juegan un papel importante. Si un objeto se coloca en una inclinación, su centro de gravedad puede cambiar, afectando su estabilidad. Por ejemplo, un libro que se sostiene verticalmente tendrá un centro de gravedad diferente al de un libro que se apoya horizontalmente sobre una mesa.
¿El centro de gravedad es siempre el mismo para un objeto?
No, el centro de gravedad de un objeto puede cambiar dependiendo de su forma, distribución de masa y posición. Por ejemplo, si un objeto se corta o se deforma, su centro de gravedad también se verá afectado.
¿Cómo afecta el centro de gravedad a la estabilidad de un objeto?
Un centro de gravedad más bajo generalmente aumenta la estabilidad de un objeto. Si el centro de gravedad se encuentra sobre la base de soporte, el objeto es menos propenso a volcarse. Por ejemplo, los coches deportivos están diseñados con un centro de gravedad bajo para mejorar su estabilidad en curvas.
¿Se puede calcular el centro de gravedad de objetos tridimensionales de la misma manera?
El concepto de centro de gravedad se extiende a objetos tridimensionales, pero el cálculo es más complejo. Se utilizan integrales y se considera el volumen del objeto en lugar del área. Sin embargo, los principios básicos son similares.
¿Qué herramientas puedo usar para calcular el centro de gravedad?
Para figuras simples, puedes usar papel y lápiz, o software de diseño asistido por computadora (CAD) para figuras más complejas. También hay aplicaciones y calculadoras en línea que pueden ayudarte a realizar estos cálculos.
¿Es necesario conocer la densidad del material para calcular el centro de gravedad?
No siempre es necesario conocer la densidad del material para calcular el centro de gravedad, especialmente en figuras geométricas simples. Sin embargo, si la figura tiene una distribución de masa variable, la densidad puede ser un factor importante a considerar.
¿Puedo calcular el centro de gravedad de un cuerpo irregular?
Sí, puedes calcular el centro de gravedad de un cuerpo irregular utilizando el método de la suma de áreas, dividiendo la figura en formas más simples, o utilizando el método de integración si es necesario. La clave está en descomponer la figura en partes manejables.
¿Qué aplicaciones tiene el cálculo del centro de gravedad?
El cálculo del centro de gravedad tiene numerosas aplicaciones en ingeniería, diseño de vehículos, arquitectura y robótica. Por ejemplo, en la construcción, se considera el centro de gravedad para garantizar que las estructuras sean estables y seguras.